What Is Msthematics And How Important It Is To The Teaching And Learning Of Mathematics. P.d.f
- Research
- Open Access
- Published:
Enhancing achievement and interest in mathematics learning through Math-Isle
Research and Practice in Technology Enhanced Learning volume 14, Article number:5 (2019) Cite this article
Abstract
Conventional teacher-led instruction remains dominant in most elementary mathematics classrooms in Taiwan. Nether such instruction, the teacher tin rarely take intendance of all students. Many students may and then go on to fall backside the standard of mathematics achievement and lose their interest in mathematics; they somewhen give up on learning mathematics. In fact, students in Taiwan generally accept lower involvement in learning mathematics compared to many other regions/countries. Thus, how to enhance students' mathematics achievement and interest are 2 major problems, especially for those low-achieving students. This paper describes how we designed a game-based learning environment, called Math-Island, by incorporating the mechanisms of a construction management game into the noesis map of the elementary mathematics curriculum. We too report an experiment conducted with 215 elementary students for 2 years, from class 2 to grade 3. In this experiment, in addition to instructor-led teaching in the classroom, students were directed to learn with Math-Isle by using their ain tablets at school and at home. Equally a result of this experiment, we found that there is an increment in students' mathematics achievement, especially in the adding and word problems. Moreover, the achievements of low-achieving students in the experimental school outperformed the low-achieving students in the control school (a command group in another school) in discussion problems. Moreover, both the low-achieving students and the high-achieving students in the experimental school maintained a rather loftier level of interest in mathematics and in the system.
Introduction
Mathematics has been regarded as a primal subject because arithmetic and logical reasoning are the footing of science and engineering science. For this reason, educational authorities emphasize students' proficiency in computational skills and problem-solving. Recently, the results of the Programme for International Educatee Assessment (PISA) and the Trends in Mathematics and Science Report (TIMSS) in 2015 (OECD 2016; Mullis et al. 2016) revealed a challenge for Taiwan. Although Taiwanese students had higher average operation in mathematics literacy compared to students in other countries, at that place was withal a significant per centum of depression-achieving students in Taiwan. Additionally, near Taiwanese students show low levels of involvement and confidence in learning mathematics (Lee 2012).
The existence of a significant percentage of low-achieving students is probably due to teacher-led pedagogy, which still dominates mathematics classrooms in most Asian countries. It should be noted that students in every classroom possess different abilities and hence demonstrate different achievements. Unfortunately, in instructor-led educational activity, all the students are required to learn from the teacher in the aforementioned way at the same footstep (Hwang et al. 2012). Low-achieving students, without sufficient fourth dimension, are forced to receive knowledge passively. Barr and Tagg (1995) pointed out that it is urgent for low-achieving students to have more opportunities to learn mathematics at their own pace. Researchers suggested ane-to-one technology (Chan et al. 2006) through which every student is equipped with a device to learn in school or at abode seamlessly. Furthermore, they can receive firsthand feedback from Math-Island, which supports their individualized learning actively and productively. Thus, this may provide more opportunities for helping low-achieving students improve their achievement.
The low-involvement trouble for well-nigh all students in Taiwan is usually accompanied by low motivation (Krapp 1999). Furthermore, students with continuously low performance in mathematics may somewhen lose their involvement and decline to learn further (Schraw et al. 2001). This is a severe problem. To motivate students to acquire, researchers design educational games to provide enjoyable and engaging learning experiences (Kiili and Ketamo 2007). Some of these researchers plant that game-based learning may facilitate students' learning in terms of motivation and learning effects (Liu and Chu 2010), spatial abilities and attending (Barlett et al. 2009), situated learning, and problem-solving (Li and Tsai 2013). Given these positive results, nosotros hope that our educational game tin enhance and sustain the educatee's interest in learning mathematics.
In fact, many researchers who endeavored to develop educational games for learning mathematics have shown that their games could facilitate mathematics operation, enjoyment, and self-efficacy (Ku et al. 2014; McLaren et al. 2017). Although some of the studies were conducted for as many as 4 months (e.thou., Hanus and Fob 2015), one may however criticize them for the possibility that the students' involvement could exist a novelty effect—meaning their interest will decrease as the feeling of novelty diminishes over time (Koivisto and Hamari 2014). Due to the limitations of either experimental fourth dimension or sample sizes, most studies could not effectively exclude the novelty effect of games, unless they were conducted in a natural setting for a long time.
In this study, nosotros collaborated with an experimental elementary schoolhouse for more than two years. The mathematics teachers in the school adopted our online educational game, Math-Isle. The students used their ain tablet PCs to learn mathematics from the game in class or at habitation at their own step. In particular, low-achieving students might take a take a chance to catch up with the other students and start to feel interested in learning mathematics. Most importantly, because the online educational game was a part of the mathematics curriculum, the students could treat the game every bit their ordinary learning materials like textbooks. In this paper, we reported a ii-yr written report, in which 215 2nd graders in the schoolhouse adopted the Math-Island game in their daily routine. More specifically, the purpose of this newspaper was to investigate the upshot of the game on students' mathematics accomplishment. Additionally, nosotros were too concerned virtually how well the depression-achieving students learned, whether they were interested in mathematics and the game, and how their interest in mathematics compared with that of high-achieving students. In such a long-term study with a large sample size, it was expected that the novelty effect would be considerably reduced, allowing us to evaluate the effect of the educational game on students' achievement and interest.
The paper is organized as follows. In the "Related works" section, nosotros review related studies on computer-supported mathematics learning and educational games. In the "Design" section, the game mechanism and the organization design are presented. In the "Method" department, we draw the research method and the procedures of this study. In the "Results" section, the enquiry results near students' accomplishment and interest are presented. In the "Word on some features of this study" section, nosotros hash out the long-term written report, noesis map blueprint, and the two game mechanisms. Finally, the summary of the electric current situation and potential futurity piece of work is described in the "Conclusion and future work" section.
Related works
Computer-supported mathematics learning
The mathematics curriculum in simple schools basically includes conceptual agreement, procedural fluency, and strategic competence in terms of mathematical proficiency (run across Kilpatrick et al. 2001). Beginning, conceptual agreement refers to students' comprehension of mathematical concepts and the relationships between concepts. Researchers have designed various computer-based scaffolds and feedback to build students' concepts and clarify potential misconceptions. For example, for guiding students' discovery of the patterns of concepts, Yang et al. (2012) adopted an anterior discovery learning approach to pattern online learning materials in which students were provided with similar examples with a critical attribute of the concept varied. McLaren et al. (2017) provided students with prompts to correct their common misconceptions most decimals. They conducted a study with the game adopted as a replacement for seven lessons of regular mathematics classes. Their results showed that the educational game could facilitate better learning performance and enjoyment than a conventional instructional approach.
Second, procedural fluency refers to the skill in conveying out calculations correctly and efficiently. For improving procedural fluency, students need to take knowledge of calculation rules (eastward.grand., place values) and practise the process without mistakes. Researchers developed various digital games to overcome the boredom of practice. For instance, Chen et al. (2012a, 2012b) designed a Cross Number Puzzle game for practicing arithmetic expressions. In the game, students could individually or collaboratively solve a puzzle, which involved extensive calculation. Their study showed that the low-power students in the collaborative condition fabricated the almost comeback in calculation skills. Ku et al. (2014) developed mini-games to railroad train students' mental adding power. They showed that the mini-games could not merely improve students' adding functioning merely as well increase their confidence in mathematics.
Tertiary, strategic competence refers to mathematical problem-solving ability, in detail, word problem-solving in elementary education. Some researchers adult multilevel calculator-based scaffolds to help students translate word problems to equations step past footstep (due east.g., González-Calero et al. 2014), while other researchers noticed the trouble of over-scaffolding. Specifically, students could exist too scaffolded and have picayune space to develop their abilities. To avoid this situation, many researchers proposed allowing students to seek help during word problem-solving (Chase and Abrahamson 2015; Roll et al. 2014). For example, Cheng et al. (2015) designed a Scaffolding Seeking system to encourage elementary students to solve word problems by themselves by expressing their thinking first, instead of receiving and potentially abusing scaffolds.
Digital educational games for mathematics learning
Because mathematics is an abstract bailiwick, elementary students hands lose interest in it, particularly low-achieving students. Some researchers tailored educational games for learning a specific set of mathematical cognition (e.k., the Decimal Points game; McLaren et al. 2017), so that students could be motivated to larn mathematics. However, if our purpose was to back up a complete mathematics curriculum for elementary schools, it seemed impractical to design various educational games for all kinds of knowledge. A feasible approach is to adopt a gamified content structure to reorganize all learning materials. For case, inspired by the design of most role-playing games, Chen et al. (2012a, 2012b) proposed a iii-tiered framework of game-based learning—a game world, quests, and learning materials—for supporting simple students' enjoyment and goal setting in mathematics learning. Furthermore, while a game earth may facilitate students' exploration and participation, quests are the containers of learning materials with specific goals and rewards. In the game globe, students receive quests from nonplayer virtual characters, who may enhance social commitments. To consummate the quests, students have to brand efforts to undertake learning materials. Today, quests have been widely adopted in the pattern of educational games (e.g., Azevedo et al. 2012; Hwang et al. 2015).
Nonetheless, in educational games with quests, students still play the role of receivers rather than active learners. To facilitate elementary students' initiative, Lao et al. (2017) designed digital learning contracts, which required students to gear up weekly learning goals at the commencement of a week and checked whether they achieved the goals at the cease of the calendar week. More than specifically, when setting weekly goals, students had to decide on the quantity of learning materials that they wanted to undertake in the coming week. Furthermore, they too had to decide the average definiteness of the tests that followed the learning materials. To help them set up reasonable and feasible goals, the organisation provided statistics from the past 4 weeks. As a result, the students may reflect on how well they learned and then make advisable decisions. After setting goals, students are provided with a series of learning materials for attempting to reach those goals. At the stop of the week, they may reverberate on whether they achieved their learning goals in the contracts. In a sense, learning contracts may not only strengthen the sense of commitment merely too empower students to take more control of their learning.
In textbooks or classrooms, learning is normally predefined every bit a specific sequence, which students must follow to learn. Still, the construction of knowledge is non linear, but a network. If nosotros could reorganize these learning materials according to the construction of knowledge, students could explore knowledge and notice the relationships among different pieces of knowledge when learning (Davenport and Prusak 2000). Knowledge mapping has the reward of providing students concrete content through explicit knowledge graphics (Ebener et al. 2006). Previous studies have shown that the incorporation of knowledge structures into educational games could finer enhance students' achievement without affecting their motivation and self-efficacy (Chu et al. 2015). For this reason, this study attempted to visualize the structure of cognition in an educational game. In other words, a knowledge map was visualized and gamified so that students could brand decisions to construct their own noesis map in games.
Design
To enhance students' mathematics achievement and interests, nosotros designed the Math-Island online game by incorporating a gamified cognition map of the elementary mathematics curriculum. More than specifically, nosotros adopt the mechanisms of a structure direction game, in which every pupil owns a virtual island (a city) and plays the function of the mayor. The goal of the game is to build their cities on the islands by learning mathematics.
System architecture
The Math-Island game is a Web awarding, supporting cross-device interactions amid students, teachers, and the mathematics content structure. The system architecture of the Math-Island is shown in Fig. 1. The pedagogical knowledge and learning materials are stored in the module of digital learning content, organized past a mathematical knowledge map. The students' portfolios near interactions and works are stored in the portfolio database and the status database. When a student chooses a goal concept in the knowledge map, the respective digital learning content is arranged and delivered to his/her browser. Besides, when the student is learning in the Math-Isle, the feedback module provides firsthand feedback (e.g., hints or scaffolded solutions) for guidance and grants rewards for encouragement. The learning results can also be shared with other classmates by the interaction module. In addition to students, their teachers can also admission the databases for the students' learning data. Furthermore, the information consists of the students' status (due east.g., learning performance or virtual accomplishment in the game) and processes (e.g., their personal learning logs). In the Math-Island, information technology is expected that students can manage their learning and monitor the learning results past the construction management mechanism. In the concurrently, teachers can also trace students' learning logs, diagnose their weaknesses from portfolio analysis, and assign students with specific tasks to improve their mathematics learning.
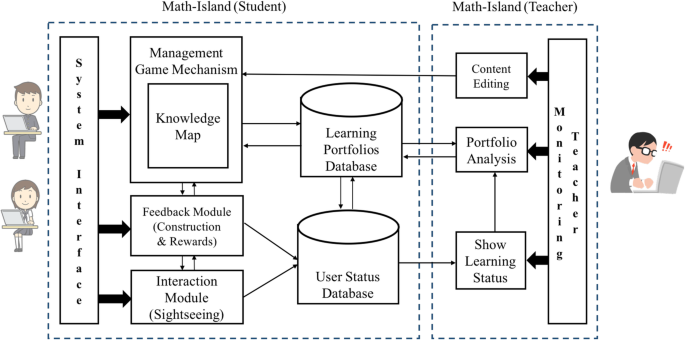
The system architecture of Math-Island
Knowledge map
To increase students' mathematics achievement, the Math-Island game targets the complete mathematics curriculum of unproblematic schools in Taiwan, which mainly contains the iv domains: numerical operation, quantity and mensurate, geometry, and statistics and probability (Ministry building of Education of R.O.C. 2003). Furthermore, every domain consists of several subdomains with corresponding concepts. For instance, the domain of numerical operation contains four subdomains: numbers, addition, and subtraction for the first and second graders. In the subdomain of subtraction, there are a series of concepts, including the meaning of subtraction, one-digit subtraction, and ii-digit subtraction. These concepts should exist learned consecutively. In the Math-Island system, the curriculum is restructured every bit a noesis map, then that they may preview the whole structure of knowledge, recall what they have learned, and realize what they will acquire.
More than specifically, the Math-Island system uses the representational metaphor of an "island," where a virtual city is located and represents the cognition map. Furthermore, the island comprises areas, roads, and buildings, which are the embodiments of domains, subdomains, and concepts in the curriculum, respectively. As shown in Fig. 2, for example, in an surface area of numeral operation in Math-Island, in that location are many roads, such as an improver route and a subtraction route. On the addition road, the commencement building should be the meaning of addition, followed by the buildings of 1-digit addition and then ii-digit addition. Students tin choose these buildings to larn mathematical concepts. In each building, the system provides a series of learning tasks for learning the specific concept. Currently, Math-Island provides elementary students with more than 1300 learning tasks from the commencement grade to the sixth grade, with more than than 25,000 questions in the tasks.
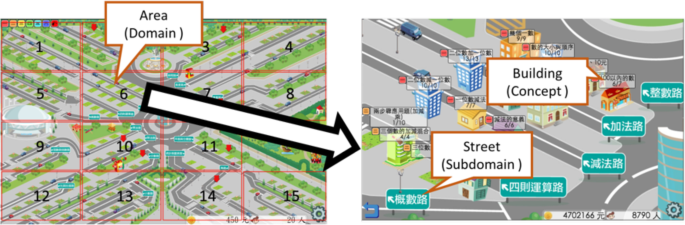
The cognition map
In Math-Isle, a learning task is an interactive page turner, including video clips and interactive exercises for conceptual agreement, calculation, and discussion problem-solving. In each task, the learning process mainly consists of 3 steps: watching demonstrations, practicing examples, and getting rewards. Commencement, students larn a mathematical concept by watching videos, in which a human tutor demonstrates examples, explains the rationale, and provides instructions. Second, students follow the instructions to respond a series of questions related to the examples in the videos. When answering questions, students are provided with firsthand feedback. Furthermore, if students input incorrect answers, the organization provides multilevel hints so that they could effigy out solutions by themselves. Finally, after completing learning tasks, students receive virtual money according to their accuracy rates in the tasks. The virtual money is used to purchase unique buildings to develop their islands in the game.
Game mechanisms
In the Math-Island game, in that location are two game mechanisms: construction and sightseeing (as shown in Fig. 3). The quondam is designed to assist students manage their learning process, whereas the latter is designed to facilitate social interaction, which may further motivate students to meliorate develop their cities. By doing and then, the Math-Island tin can be regarded every bit one'south learning portfolio, which is a complete record that purposely collects data about i's learning processes and outcomes (Arter and Spandel 2005). Furthermore, learning portfolios are a valuable enquiry tool for gaining an agreement about personal accomplishments (Birgin and Baki 2007), because learning portfolios tin can display one's learning process, mental attitude, and growth later on learning (Lin and Tsai 2001). The advent of the isle reflects what students have learned and accept not learned from the knowledge map. When students observe their learning status in an interesting style, they may be concerned about their learning condition with the enhanced awareness of their learning portfolios. By keeping all activity processes, students tin can reflect on their efforts, growth, and achievements. In a sense, with the game mechanisms, the knowledge map can be regarded as a manipulatable open learner model, which not only represents students' learning status but besides invites students to improve it (Vélez et al. 2009).
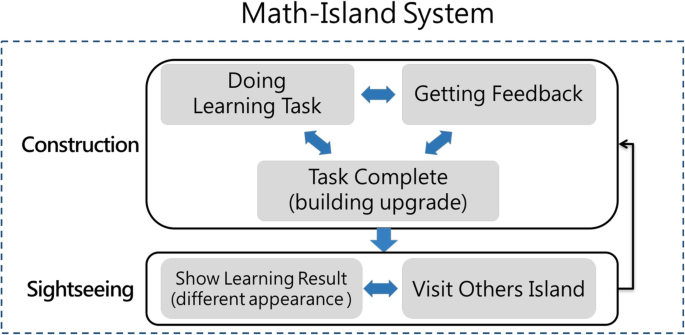
Two game mechanisms for Math-Island
Start, the structure mechanism allows students to program and manage their cities by constructing and upgrading buildings. To do so, they have to determine which buildings they desire to construct or upgrade. Then, they are required to consummate corresponding learning tasks in the building to determine which levels of buildings they can construct. As shown in Fig. 4, the levels of buildings depend on the completeness of a certain concept, compared with the thresholds. For instance, when students complete one third of the learning tasks, the first level of a building is synthetic. Later, when they complete ii thirds of the tasks, the building is upgraded to the second level. After completing all the tasks in a building, they also consummate the concluding level and are allowed to construct the next building on the road. Conversely, if students failed the lowest level of the threshold, they might demand to picket the video and/or practise the learning tasks once more. Past doing so, students tin make their plans to construct the buildings at their ain pace. When students manage their cities, they actually attempt to ameliorate their learning condition. In other words, the structure mechanism offers an alternative manner to guide students to regulate their learning efforts.
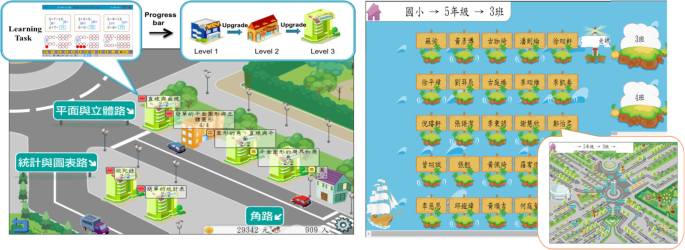
Screenshots of construction and sightseeing mechanisms in Math-Island
Second, the sightseeing mechanism provides students with a social phase to evidence other students how well their Math-Islands have been built. This mechanism is implemented as a public space, where other students play the part of tourists who visit Math-Island. In other words, this sightseeing machinery harnesses social interaction to improve individual learning. As shown in Fig. 4, because students tin can construct different areas or roads, their islands may take different appearances. When students visit a well-adult Math-Island, they might take a positive impression, which may facilitate their self-reflection. Accordingly, they may be willing to expend more than effort to improve their isle. On the other mitt, the student who owns the isle may too be encouraged to develop their island meliorate. Furthermore, when students meet that they accept a completely constructed edifice on a road, they may perceive that they are good at these concepts. Conversely, if their buildings are small, the students may realize their weaknesses or difficulties in these concepts. Appropriately, they may be willing to brand more than attempt for improvement. On the other hand, the student who owns the isle may also be encouraged to develop their isle better. In a discussion, the visualization may play the role of stimulators, and so that students may be motivated to improve their learning condition.
Method
This paper reported a two-year report in which the Math-Isle organization was adopted in an elementary schoolhouse. The report addressed the following 2 inquiry questions: (1) Did the Math-Isle arrangement facilitate students' mathematics achievement in terms of conceptual understanding, calculating, and word trouble-solving? In detail, how was the mathematics achievement of the low-achieving students? (2) What was students' levels of involvement in mathematics and the system, particularly that of low-achieving students?
Participants
The study, conducted from June 2013 to June 2015, included 215 second graders (98 females and 117 males), whose average age was 8 years erstwhile, in an unproblematic school located in a suburban region of a northern city in Taiwan. The school had collaborated with our inquiry team for more than than 2 years and was thus chosen as an experimental school for this study. In this school, approximately ane tertiary of the students came from families with a low or middle level of socioeconomic status. Information technology was expected that the lessons learned from this written report could be applicable to other schools with similar educatee populations in the future. The parents were supportive of this program and willing to provide personal tablets for their children (Liao et al. 2017). By doing then, the students in the experimental school were able to employ their tablets to access the Math-Island system as a learning tool at both schoolhouse and abode. To compare the students' mathematics accomplishment with a baseline, this study also included 125 second graders (63 females and 62 males) from another school with similar socioeconomic backgrounds in the aforementioned region of the metropolis as a control school. The students in the control school received but conventional mathematics teaching without using the Math-Island arrangement during the 2-year period.
Procedure
Before the first semester, a 3-week training workshop was conducted to familiarize the students with the basic operation of tablets and the Math-Island system. By doing so, it was ensured that all participants had like prerequisite skills. The procedure of this report was illustrated in Table ane. At the get-go of the first semester, a mathematics achievement assessment was conducted as a pretest in both the experimental and the control school to examine the students' initial mathematics ability as 2d graders. From June 2013 to June 2015, while the students in the command school learned mathematics in a conventional way, the students in the experimental schoolhouse learned mathematics non only in mathematics classes but as well through the Math-Island arrangement. Although the teachers in the experimental school mainly adopted lectures in mathematics classes, they used the Math-Island organization as learning materials at school and for homework. At the same time, they allowed the students to explore the knowledge map at their own footstep. During the 2 years, every student completed 286.78 learning tasks on average, and each task took them viii.86 min. Given that there were 344 tasks for the 2d and third graders, the students could stop 83.37% of tasks according to the standard progress. The data also showed that the average correctness rate of the students was 85.75%. At the finish of the second year, some other mathematics accomplishment cess was administered as a posttest in both schools to evaluate students' mathematics ability equally third graders. Additionally, an involvement questionnaire was employed in the experimental schoolhouse to collect the students' perceptions of mathematics and the Math-Isle organisation. To understand the teachers' opinions of how they experience about the students using the system, interviews with the teachers in the experimental school were also conducted.
Data collection
Mathematics achievement assessment
To evaluate the students' mathematics ability, this study adopted a standardized achievement cess of mathematics ability (Lin et al. 2009), which was developed from a random sample of elementary students from different counties in Taiwan to serve as a norm with appropriate reliability (the internal consistency was 0.85, and the examination-retest reliability was 0.86) and validity (the correlation by domain experts in content validity was 0.92, and the concurrent validity was 0.75). As a pretest, the assessment of the second graders consisted of 50 items, including conceptual understanding (23 items), computing (18 items), and word problem-solving (9 items). Every bit a posttest, the cess of the third graders consisted of lx items, including conceptual understanding (18 items), calculating (27 items), and word trouble-solving (15 items). The scores of the test ranged from 0 to 50 points. Because some students were absent during the test, this study obtained 209 valid tests from the experimental schoolhouse and 125 tests from the command school.
Interest questionnaire
The interest questionnaire comprised ii parts: students' interest in mathematics and the Math-Island arrangement. Regarding the kickoff role, this study adopted items from a mathematics questionnaire of PISA and TIMSS 2012 (OECD 2013; Mullis et al. 2012), the reliability of which was sound. This role included three dimensions: attitude (14 items, Cronbach's alpha = .83), initiative (17 items, Cronbach'due south blastoff = .82), and conviction (xiv items Cronbach's blastoff = .72). Furthermore, the dimension of attitude was used to assess the tendency of students' view on mathematics. For example, a sample item of attitudes was "I am interested in learning mathematics." The dimension of initiatives was used to assess how students were willing to larn mathematics actively. A sample item of initiatives was "I keep studying until I sympathize mathematics materials." The dimension of confidences was used to assess students' perceived mathematics abilities. A sample item was "I am confident well-nigh calculating whole numbers such equally iii + 5 × 4." These items were translated to Chinese for this study. Regarding the second part, this written report adopted self-fabricated items to assess students' motivations for using the Math-Island organization. This office included two dimensions: attraction (viii items) and satisfaction (5 items). The dimension of allure was used to assess how well the arrangement could attract students' attention. A sample detail was "I experience Math-island is very highly-seasoned to me." The dimension of satisfaction was used to assess how the students felt after using the system. A sample item was "I felt that upgrading the buildings in my Math-Island brought me much happiness." These items were assessed according to a 4-point Likert calibration, ranging from "strongly disagreed (i)," "disagreed (ii)," "agreed (three)," and "strongly agreed (4)" in this questionnaire. Due to the absences of several students on the day the questionnaire was administered, there were simply 207 valid questionnaires in this study.
Instructor interview
This study besides included teachers' perspectives on how the students used the Math-Island system to learn mathematics in the experimental school. This function of the study adopted semistructured interviews of eight teachers, which comprised the following three main questions: (a) Practice you take any notable stories about students using the Math-Island system? (b) Regarding Math-Island, what are your teaching experiences that can be shared with other teachers? (c) Do you take any suggestions for the Math-Island system? The interview was recorded and transcribed verbatim. The transcripts were coded and categorized according to the five dimensions of the questionnaire (i.eastward., the attitude, initiative, and confidence about mathematics, as well equally the attraction and satisfaction with the system) equally additional prove of the students' involvement in the experimental schoolhouse.
Data analysis
For the first inquiry question, this written report conducted a multivariate analysis of variance (MANOVA) with the schools every bit a between-subject variable and the students' scores (conceptual understanding, computing, and word problem-solving) in the pre/posttests as dependent variables. Moreover, this written report also conducted a MANOVA to compare the depression-achieving students from both schools. In addition, the tests were also carried out to compare achievements with the norm (Lin et al. 2009). For the 2d research question, several z tests were used to examine how the interests of the low-achieving students were distributed compared with the whole sample. Teachers' interviews were besides adopted to back up the results of the questionnaire.
Results
Mathematics achievement
To examine the homogeneity of the students in both schools in the get-go year, the MANOVA of the pretest was conducted. The results, every bit shown in Table 2, indicated that there were no significant differences in their initial mathematics achievements in terms of conceptual agreement, calculating, and word problem-solving (Wilks' λ = 0.982, F(3330) = two.034, p > 0.05). In other words, the students of both schools had similar mathematics abilities at the time of the first mathematics achievement assessment and could be fairly compared.
At the end of the fourth course, the students of both schools received the posttest, the results of which were examined by a MANOVA. Equally shown in Tabular array iii, the effect of the posttest on students' mathematics achievement was pregnant (Wilks' λ = 0.946, p < 0.05). The results suggested that the students who used Math-Island for two years had improve mathematics abilities than those who did non. The analysis further revealed that the univariate effects on calculating and word problem-solving were significant, just the effect on conceptual agreement was insignificant. The results indicated that the students in the experimental school outperformed their counterparts in terms of the process and awarding of arithmetics. The reason may be that the system provided students with more than opportunities to do adding exercises and word problems, and the students were more willing to do these exercises in a game-based environment. Furthermore, they were engaged in solving various exercises with the back up of firsthand feedback until they passed the requirements of every building in their Math-Island. However, the students learned mathematical concepts mainly by watching videos in the system, which provided only demonstrations like lectures in conventional classrooms. For this reason, the result of the system on conceptual agreement was similar to that of teachers' conventional instruction.
Furthermore, to examine the differences between the depression-achieving students in both schools, another MANOVA was also conducted on the pretest and the posttest. The pretest results indicated that there were no meaning differences in their initial mathematics achievement in terms of conceptual understanding, calculating, and word problem-solving (Wilks' λ = 0.943, F(3110) = 2.210, p > 0.05).
The MANOVA analysis of the posttest is shown in Tabular array iv. The results showed that the upshot of the arrangement on the mathematics accomplishment of depression-achieving students was significant (Wilks' λ = 0.934, p < 0.05). The analysis further revealed that but the univariate effect on word trouble-solving was pregnant. The results suggested that the low-achieving students who used Math-Isle for 2 years had better discussion problem-solving ability than those students in the control school, but the result on conceptual understanding and procedural fluency was insignificant. The results indicated that the Math-Island system could finer enhance low-achieving students' ability to solve discussion problems.
Because the mathematics achievement assessment was a standardized achievement assessment (Lin et al. 2009), the research team did a further analysis of the assessments past comparing the results with the norm. In the pretest, the average score of the control schoolhouse was the percentile rank of a score (PR) 55, but their boilerplate score surprisingly decreased to PR 34 in the posttest. The results confirmed the fact that conventional mathematics teaching in Taiwan might result in an K-shape distribution, suggesting that low-achieving students required boosted learning resources. Conversely, the average score of the experimental school was PR 48 in the pretest, and their score slightly decreased to PR 44 in the posttest. Overall, both PR values were decreasing, considering the mathematics curriculum became more than and more hard from the second form to the fourth grade. However, it should be noted that the experimental schoolhouse has been less affected, resulting in a meaning departure compared with the control school (see Tabular array 5). Notably, the average score of word trouble-solving in the posttest of the experimental school was PR 64, which was significantly college than the nationwide norm (z = twenty.8, p < .05). The results were consistent with the univariate effect of the MANOVA on discussion trouble-solving, suggesting that the Math-Island system could aid students larn to complete discussion problems improve. This may be because the learning tasks in Math-Island provided students with acceptable explanations for diverse types of discussion problems and provided feedback for exercises.
Interest
To examine whether the low-achieving students had low levels of interest in mathematics and the Math-Isle arrangement, the study adopted z tests on the information of the involvement questionnaire. Table five shows the descriptive statistics and the results of the z tests. Regarding the interest in mathematics, the analysis showed that the interest of the low-achieving students was like to that of the whole sample in terms of attitude, initiative, and confidence. The results were unlike from previous studies asserting that low-achieving students tended to have lower levels of interest in mathematics (Al-Zoubi and Younes 2015). The reason was peradventure that the low-achieving students were comparably motivated to learn mathematics in the Math-Island system. Equally a outcome, a teacher (#T-301) said, "some students would like to go to Math-Island after schoolhouse, and a handful of students could even consummate up to forty tasks (in a day)," implying that the students had a positive attitude and initiative related to learning mathematics.
Some other teacher (T-312) also indicated "some students who were frustrated with math could regain confidence when receiving the feedback for correct answers in the bones tasks. Cheers to this, they would non feel high-pressure when moving on to current lessons." In a sense, the immediate feedback provided the depression-achieving students with sufficient back up and may encourage them to persistently learn mathematics. Furthermore, by learning individually after course, they could effectively prepare themselves for futurity learning. The results suggested that the system could serve every bit a scaffolding on conventional instruction for depression-achieving students. The students could benefit from such a blended learning environment and, thus, build confidence in mathematics past learning at their own paces.
The low-achieving students as a whole were also attracted to the system and felt satisfaction from it. Teacher (#T-307) said that, "In that location was a hyperactive and mischievous student in my grade. However, when he was alone, he would get on to Math-Island, concentrating on the tasks quietly. He gradually came to enjoy learning mathematics. It seemed that Math-Island was more attractive to them than a lecture by a teacher. I believed that students could be encouraged, thus improve their power and learn happily." Another teacher (#T-304) farther pointed out that, "For students, they did not only feel similar they were learning mathematics because of the game-based user interface. Conversely, they enjoyed the delectation when completing a task, as if they were going aboard to join a contest." In teachers' opinions, such a game-based learning environs did not disturb their instruction. Instead, the system could help the teachers concenter students' attention and motivate them to larn mathematics actively considering of its highly-seasoned game and joyful learning tasks. Furthermore, continuously overcoming the tasks might bring students a sense of achievement and satisfaction.
Word on some features of this study
In add-on to the enhancement of achievement and interest, we noticed that there are some features in this study and our design worth some give-and-take.
The advantages of edifice a long-term study
Owing to the limitations of deployment time and sample sizes, it is hard for almost researchers to acquit a longitudinal written report. Fortunately, we had a gamble to maintain a long-term collaboration with an experimental school for more than 2 years. From this experiment, we discover that there are two advantages to conducting a long-term written report.
Obtaining substantial evidence from the game-based learning surroundings
The enquiry environment was a natural setting, which could not exist entirely controlled and manipulated similar well-nigh experiments in laboratories. Nevertheless, this study could provide long-term bear witness to investigate how students learned in a game-based learning surroundings with their tablets. It should be noted that nosotros did not aim to supplant teachers in classrooms with the Math-Island game. Instead, nosotros attempted to plant an ordinary learning scenario, in which the teachers and students regarded the game equally 1 of the learning resources. For instance, teachers may help low-achieving students to improve their understanding of a specific concept in the Math-Island system. When students are learning mathematics in the Math-Island game, teachers may take the game as a formative assessment and locate students' difficulties in mathematics.
Supporting teachers' instructions and facilitating students' learning
The long-term study non only proved the effectiveness of Math-Island but as well offered researchers an opportunity to make up one's mind teachers' roles in such a computer-supported learning surround. For example, teachers may encounter difficulties in dealing with the progress of both high- and depression-achieving students. How do they take care of all students with different abilities at the same fourth dimension? Future teachers may require more teaching strategies in such a cocky-directed learning environment. Digital technology has an advantage in helping teachers manage students' learning portfolios. For example, the arrangement can go on track of all the learning activities. Furthermore, the organisation should provide teachers with monitoring functions so that they know the average status of their class's and individuals' learning progress. Yet, information technology is still a challenge for researchers to develop a well-designed visualization tool to support teachers' understanding of students' learning conditions and their option of appropriate teaching strategies.
Incorporating a gamified noesis map of the elementary mathematics curriculum
Providing choices of learning paths
Math-Island uses a representational metaphor of an "island," where a virtual city is located and represents the knowledge map. Furthermore, the island comprises areas, roads, and buildings, which are the embodiments of domains, subdomains, and concepts in the curriculum, respectively. Because the gamified knowledge map provides students with multiple virtual roads to acquire in the system, every student may take different routes. For instance, some students may be more than interested in geometry, while others may exist confident in exploring the rules of arithmetics. In this study, we noticed that the low-achieving students needed more time to work on basic tasks, while high-achieving students easily passed those tasks and moved on to the next ones. As a result, some of the high-achieving students had already started to learn the materials for the next grade level. This was possibly because high-achieving students were able to respond well to challenging assignments (Singh 2011). Therefore, nosotros should provide high-achieving students with more complex tasks to maintain their interest. For example, Math-Island should provide some authentic mathematical problems as advanced exercises.
Visualizing the learning portfolio
In this study, we demonstrated a long-term instance of incorporating a gamified noesis map in an simple mathematical curriculum. In the Math-Island game, the curriculum is visualized as a knowledge map instead of a linear sequence, as in textbooks. By doing then, students are enabled to explore relationships in the mathematics curriculum represented by the cognition map; that is, the structure of the different roads on Math-Isle. Furthermore, before learning, students may preview what will be learned, and afterward learning, students may also reflect on how well they learned. Unlike traditional lectures or textbooks, in which students could only follow a predefined lodge to learn cognition without thinking why they have to learn it, the knowledge map allows students to understand the construction of knowledge and program how to achieve avant-garde knowledge. Although the order of knowledge still remains the same, students take primary command of their learning. In a sense, the knowledge map may liberate elementary students from passive learning.
Adopting the mechanisms of a structure direction game
This two-year written report showed that the adaptation of 2 game mechanisms, construction and sightseeing, into the elementary mathematical curriculum could effectively better students' learning achievement. The reason may be that students probable developed interests in using Math-Isle to learn mathematics actively, regardless of whether they are loftier- and depression-achieving students.
Gaining a sense of achievement and ownership through the construction mechanism
Regardless of the structure mechanism, Math-Isle allows students to plan and manage their cities past amalgam and upgrading buildings. Math-Island took the advantages of construction direction games to facilitate simple students' active participation in their mathematical learning. Furthermore, students may manage their noesis by planning and constructing of buildings on their virtual islands. Like most construction direction games, students prepare goals and brand decisions so that they may accrue their assets. These avails are not only external rewards only also visible achievements, which may bring a sense of buying and conviction. In other words, the system gamified the process of cocky-directed learning.
Demonstrating learning issue to peers through the sightseeing mechanism
As for the sightseeing machinery, in conventional teaching, elementary students usually lack the self-control to learn noesis actively (Duckworth et al. 2014) or require a social stage to prove other students, resulting in low achievement and motivation. On the other manus, although previous researchers have already proposed various cocky-regulated learning strategies (such as Taub et al. 2014), it is still hard for children to keep adopting specific learning strategies for a long fourth dimension. For these reasons, this study uses the sightseeing mechanism to engage uncomplicated students in a social stage to prove other students how well their Math-Islands have been built. For example, in Math-Isle, although the students think that they construct buildings in their islands, they programme the development of their knowledge maps. Later on learning, they may likewise reflect on their progress by observing the appearance of the buildings.
In brief, owing to the construction machinery, the students are allowed to choose a place and build their unique islands by learning concepts. During the process, students take to do the learning task, become feedback, and get rewards, which are the three major functions of the construction functions. In the sightseeing machinery, students' unique islands (learning result) can be shared and visited by other classmates. The student's Math-Island thus serves as a stage for showing off their learning results. The two mechanisms offer an incentive model connected to the game mechanism'south forming a positive bike: the more the students learn, the more than unique islands they can build, with more visitors.
Conclusion and future work
This study reported the results of a 2-year experiment with the Math-Island system, in which a knowledge map with extensive mathematics content was provided to back up the complete uncomplicated mathematics curriculum. Each route in Math-Isle represents a mathematical topic, such every bit addition. There are many buildings on each route, with each building representing a unit of the mathematics curriculum. Students may learn about the concept and practice information technology in each edifice while being provided with feedback by the system. In addition, the construction management online game machinery is designed to enhance and sustain students' involvement in learning mathematics. The aim of this study was non only to examine whether the Math-Isle arrangement could ameliorate students' achievements simply also to investigate how much the depression-achieving students would exist interested in learning mathematics after using the system for 2 years.
As for enhancing achievement, the result indicated that the Math-Island system could finer amend the students' ability to calculate expressions and solve discussion problems. In detail, the depression-achieving students outperformed those of the norm in terms of word problem-solving. For enhancing interest, we constitute that both the low-achieving and the high-achieving students in the experimental school, when using the Math-Island system, maintained a rather high level of interest in learning mathematics and using the organisation. The results of this study indicated some possibility that elementary students could exist able to learn mathematics in a self-directed learning fashion (Nilson 2014; Chen et al. 2012a, b) under the Math-Isle environment. This possibility is worthy of futurity exploration. For case, past analyzing pupil data, we tin investigate how to support students in conducting cocky-directed learning. Additionally, because we have already collected a considerable amount of educatee data, we are currently employing automobile learning techniques to improve feedback to the students. Finally, to provide students appropriate challenges, the diversity, quantity, and difficulty of content may need to be increased in the Math-Isle arrangement.
Abbreviations
- PISA:
-
Plan for International Student Assessment
- PR:
-
The percentile rank of a score
- TIMSS:
-
Trends in Mathematics and Scientific discipline Written report
References
-
Al-Zoubi, S. Thou., & Younes, Grand. A. B. (2015). Low academic achievement: causes and results. Theory and Practice in Language Studies, 5(11), 2262.
-
Arter, J. A., & Spandel, 5. (2005). Using portfolios of student piece of work in instruction and assessment. Educational Measurement Problems and Practice, eleven(1), 36–44.
-
Azevedo, R., Feyzi-Behnagh, R., Duffy, M., Harley, J., & Trevors, Grand. (2012). Metacognition and self-regulated learning in student-centered leaning environments. In D. Jonassen & S. Land (Eds.), Theoretical foundations of student-centered learning environments (pp. 171–197). New York: Routledge.
-
Barlett, C. P., Anderson, C. A., & Swing, E. 50. (2009). Video game effects confirmed, suspected and speculative: a review of the evidence. Simulation & Gaming, 40(3), 377–403.
-
Barr, R. B., & Tagg, J. (1995). From teaching to learning—a new epitome for undergraduate education. Change The Magazine of College Learning, 27(6), 12–26.
-
Birgin, O., & Baki, A. (2007). The use of portfolio to appraise student'southward functioning. Periodical of Turkish Science Educational activity, iv(2), 75–90.
-
Chan, T. W., Roschelle, J., Hsi, S., Kinshuk, Sharples, Thousand., Brown, T., et al. (2006). Ane-to-one engineering science-enhanced learning: an opportunity for global research collaboration. Research and Practice in Technology Enhanced Learning, 1(01), iii–29.
-
Hunt, One thousand., & Abrahamson, D. (2015). Contrary-scaffolding algebra: empirical evaluation of blueprint compages. ZDM Mathematics Education, 47(7), 1195–1209.
-
Chen, Y. H., Looi, C. K., Lin, C. P., Shao, Y. J., & Chan, T. West. (2012a). Utilizing a collaborative cantankerous number puzzle game to develop the calculating ability of addition and subtraction. Educational Technology & Society, 15(one), 354–366.
-
Chen, Z. H., Liao, C. C., Cheng, H. N., Yeh, C. Y., & Chan, T. West. (2012b). Influence of game quests on pupils' enjoyment and goal-pursuing in math learning. Periodical of Educational Applied science & Society, 15(2), 317–327.
-
Cheng, H. North. H., Yang, E. F. Y., Liao, C. C. Y., Chang, B., Huang, Y. C. Y., & Chan, T. W. (2015). Scaffold seeking: a reverse design of scaffolding in calculator-supported word problem solving. Journal of Educational Calculating Research, 53(3), 409–435.
-
Chu, H. C., Yang, K. H., & Chen, J. H. (2015). A time sequence-oriented concept map approach to developing educational computer games for history courses. Interactive Learning Environments, 23(2), 212–229.
-
Davenport, T. H. & Prusak, L. (2000). Working cognition: How organizations manage what they know. Boston: Harvard Business Schoolhouse Printing.
-
Duckworth, A. L., Gendler, T. Southward., & Gross, J. J. (2014). Self-command in school-historic period children. Educational Psychologist, 49(3), 199–217.
-
Ebener, South., Khan, A., Shademani, R., Compernolle, L., Beltran, Thousand., Lansang, M. A., & Lippman, M. (2006). Cognition mapping as a technique to support noesis translation. Message of the World Wellness Organization, 84, 636–642.
-
González-Calero, J. A., Arnau, D., Puig, L., & Arevalillo-Herráez, G. (2014). Intensive scaffolding in an intelligent tutoring arrangement for the learning of algebraic word problem solving. British Periodical of Educational Applied science, 46(half-dozen), 1189–1200.
-
Hanus, M. D., & Pull a fast one on, J. (2015). Assessing the effects of gamification in the classroom: a longitudinal study on intrinsic motivation, social comparing, satisfaction, effort, and academic performance. Computers & Teaching, eighty, 152–161.
-
Hwang, Grand. J., Chiu, L. Y., & Chen, C. H. (2015). A contextual game-based learning approach to improving students' inquiry-based learning operation in social studies courses. Computers & Education, 81, 13–25.
-
Hwang, G. J., Su, J. M., & Chen, N. Southward. (2012). E-learning introduction and practise. Taiwan: Drmaste.
-
Kiili, 1000., & Ketamo, H. (2007). Exploring the learning mechanism in educational games. Periodical of Computing and It, 15(iv), 319–324.
-
Kilpatrick, J., Swafford, J., & Findell, B. (Eds.). (2001). Adding it upwards: helping children larn mathematics. Washington, DC: National Academies Printing.
-
Koivisto, J., & Hamari, J. (2014). Demographic differences in perceived benefits from gamification. Computers in Human Behavior, 35, 179–188.
-
Krapp, A. (1999). Involvement, motivation and learning: an educational-psychological perspective. European Journal of Psychology of Education, xiv(1), 23–xl.
-
Ku, O., Chen, S. Y., Wu, D. H., Lao, A. C., & Chan, T. W. (2014). The furnishings of game-based learning on mathematical confidence and performance: high power vs. depression ability. Journal of Educational Technology & Lodge, 17(3), 65–78.
-
Lao, A. C. C., Cheng, H. Due north., Huang, One thousand. C., Ku, O., & Chan, T. W. (2017). Examining motivational orientation and learning strategies in estimator-supported self-directed learning (CS-SDL) for mathematics: the perspective of intrinsic and extrinsic goals. Periodical of Educational Computing Enquiry, 54(8), 1168–1188.
-
Lee, Y. G. (2012). Discriminating math low-accomplishment motivation patterns: comparison disadvantaged and other students in elementary and junior high school. Journal of Research in Education Sciences, 57(4), 39–71. https://doi.org/10.3966/2073753X2012125704002.
-
Li, M.-C., & Tsai, C.-C. (2013). Game-based learning in science education: a review of relevant enquiry. Journal of Science Teaching and Engineering science, 22(6), 877–898. https://doi.org/ten.1007/s10956-013-9436-x.
-
Liao, C. C., Cheng, H. N., Chang, W. C., & Chan, T. W. (2017). Supporting parental date in a BYOD (bring your own device) school. Journal of Computers in Education, four(2), 107–125.
-
Lin, B. G., Li, R. P., & Huang, Y. Z. (2009). Instructional manual of mathematical ability test for the schoolhouse-aged. Taipei: Ministry of Education.
-
Lin, P. J., & Tsai, W. H. (2001). Using enquiry-based cases to enhance prospective teachers' understanding of educational activity mathematics and their reflections. In F. Fifty. Lin (Ed.), Mutual sense in mathematics education. Proceedings of 2001 the Netherlands and Taiwan Conference on Common Sense in Mathematics Instruction (pp. 231–272). Taipei: Taiwan.
-
Liu, T. Y., & Chu, Y. L. (2010). Using ubiquitous games in an English listening and speaking course: impact on learning outcomes and motivation. Computers & Education, 55(2), 630–643. https://doi.org/10.1016/j.compedu.2010.02.023.
-
McLaren, B. Thousand., Adams, D. Thou., Mayer, R. Due east., & Forlizzi, J. (2017). A computer-based game that promotes mathematics learning more than a conventional approach. International Journal of Game-Based Learning, 7(i), 36–56.
-
Ministry of Pedagogy. (2003). Guidelines of grades 1-ix curriculum of elementary and inferior high school pedagogy. Retrieved from https://www.k12ea.gov.tw/92_sid17/%E6%96%B0%E7%B8%BD%E7%B6%B1%E8%8B%B1%E6%96%87%E7%89%88.pdf.
-
Mullis, I. V. Due south., Martin, Thou. O., Foy, P., & Drucker, K. T. (2012). PIRLS 2011 international results in reading. Chestnut Loma: TIMSS & PIRLS International Report Middle, Boston College.
-
Mullis, I. Five. S., Martin, M. O., Foy, P., & Hooper, M. (2016). TIMSS 2015 International Results in Mathematics. Retrieved from http://timssandpirls.bc.edu/timss2015/international-results/
-
Nilson, L. B. (2014). The secret of cocky-regulated learning. In Invited article for Kinesthesia Focus: Higher Ed Teaching Strategies from Magna Publications.
-
OECD. (2013). PISA 2012 results in focus: what 15-yr-olds know and what they can do with what they know: key results from PISA 2012.
-
OECD. (2016). PISA 2015 results in focus. Retrieved from: https://world wide web.oecd.org/pisa/pisa-2015-results-in-focus.pdf.
-
Roll, I., Baker, R. Due south. J. D., Aleven, V., & Koedinger, K. R. (2014). On the benefits of seeking (and avoiding) assist in online trouble-solving environments. Journal of the Learning Sciences, 23(iv), 537–560.
-
Schraw, Thousand., Flowerday, T., & Lehman, Southward. (2001). Increasing situational interest in the classroom. Educational Psychology Review, 13(3), 211–224.
-
Singh, 1000. (2011). Study of accomplishment motivation in relation to academic achievement of students. International Journal of Educational Planning and Administration, ane(2), 161–171.
-
Taub, Thousand., Azevedo, R., Bouchet, F., & Khosravifar, B. (2014). Can the use of cognitive and metacognitive self-regulated learning strategies be predicted by learners' levels of prior knowledge in hypermedia-learning environments? Computers in Homo Beliefs, 39, 356–367.
-
Vélez, J., Fabregat, R., Bull, South., & Hueva, D. (2009). The potential for open up learner models in adaptive virtual learning environments. In S. D. Craig & D. Dicheva (Eds.), AIED 2009: 14th International Conference on Artificial Intelligence in Education Workshops Proceedings Volume 8 (pp. 11–20). Brighton: International AIED Gild.
-
Yang, E. F. Y., Cheng, H. Northward. H., Ching, Eastward., & Chan, T. W. (2012). Variation based discovery learning design in i to 1 mathematics classroom. In G. Biswas, L.-H. Wong, T. Hirashima, & W. Chen (Eds.), Proceedings of the 20th International Conference on Computers in Education (pp. 811–815). Singapore: Asia-Pacific Guild for Computers in Educational activity.
Acknowledgements
Funding
The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The authors would like to thank the Ministry of Science and Technology of the Republic of Mainland china, Taiwan, for fiscal support (MOST 106-2511-Due south-008-003-MY3), and Inquiry Centre for Science and Technology forLearning, National Central Academy, Taiwan.
Availability of information and materials
As a series of subsequent research papers are all the same in progress, for now, information technology is temporarily impossible to share research data sets.
Writer information
Authors and Affiliations
Contributions
CYCY contributed to the report pattern, data conquering and assay, mainly drafted the manuscript and execution project. HNHC was involved in data conquering, revision of the manuscript and data analysis.ZHC was contributed to the study idea and drafted the manuscript. CCYL of this research was involved in data conquering and revision of the manuscript. TWC was project manager and revision of the manuscript. All authors read and approved the final manuscript.
Respective author
Ideals declarations
Authors' data
Charles Y.C. Yeh is currently an PhD pupil in Graduate Institute of Network Learning Technology at National Fundamental University. The inquiry interests include one-to-one learning environments and game-based learning.
Hercy Northward. H. Cheng is currently an associate professor and researcher in National Technology Research Center for E-Learning at Fundamental Red china Normal University, Prc. His research interests include one-to-i learning environments and game-based learning.
Zhi-Hong Chen is an acquaintance professor in Graduate Institute of Data and Computer Education at National Taiwan Normal University. His research interests focus on learning engineering and interactive stories, technology intensive linguistic communication learning and game-based learning.
Calvin C. Y. Liao is currently an Assistant Professor and Dean's Special Assistant in Higher of Nursing at National Taipei University of Nursing and Health Sciences in Taiwan. His research focuses on computer-based language learning for master schools. His current research interests include a game-based learning environment and smart technology for caregiving & wellbeing.
Tak-Wai Chan is Chair Professor of the Graduate Found of Network Learning Technology at National Primal Academy in Taiwan. He has worked on diverse areas of digital technology supported learning, including artificial intelligence in didactics, computer supported collaborative learning, digital classrooms, online learning communities, mobile and ubiquitous learning, digital game based learning, and, most recently, technology supported mathematics and language arts learning.
Competing interests
The authors declare that they have no competing interests.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed nether the terms of the Artistic Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you requite appropriate credit to the original author(south) and the source, provide a link to the Artistic Commons license, and indicate if changes were made.
Reprints and Permissions
Most this article
Cite this article
Yeh, C.Y.C., Cheng, H.Due north.H., Chen, ZH. et al. Enhancing achievement and interest in mathematics learning through Math-Isle. RPTEL 14, five (2019). https://doi.org/ten.1186/s41039-019-0100-nine
-
Received:
-
Accepted:
-
Published:
-
DOI : https://doi.org/x.1186/s41039-019-0100-9
Keywords
- Mathematics learning
- Knowledge map
- Game-based learning
- Construction direction games
What Is Msthematics And How Important It Is To The Teaching And Learning Of Mathematics. P.d.f,
Source: https://telrp.springeropen.com/articles/10.1186/s41039-019-0100-9
Posted by: smithupyrairow.blogspot.com


0 Response to "What Is Msthematics And How Important It Is To The Teaching And Learning Of Mathematics. P.d.f"
Post a Comment