How To Use Scikit Learn Mlp
1.17. Neural network models (supervised)¶
Warning
This implementation is not intended for large-scale applications. In particular, scikit-learn offers no GPU support. For much faster, GPU-based implementations, equally well as frameworks offer much more flexibility to build deep learning architectures, come across Related Projects.
ane.17.ane. Multi-layer Perceptron¶
Multi-layer Perceptron (MLP) is a supervised learning algorithm that learns a function \(f(\cdot): R^1000 \rightarrow R^o\) by training on a dataset, where \(chiliad\) is the number of dimensions for input and \(o\) is the number of dimensions for output. Given a set of features \(X = {x_1, x_2, ..., x_m}\) and a target \(y\), it can learn a non-linear function approximator for either classification or regression. It is unlike from logistic regression, in that betwixt the input and the output layer, there can be one or more than non-linear layers, called hidden layers. Figure 1 shows a one subconscious layer MLP with scalar output.
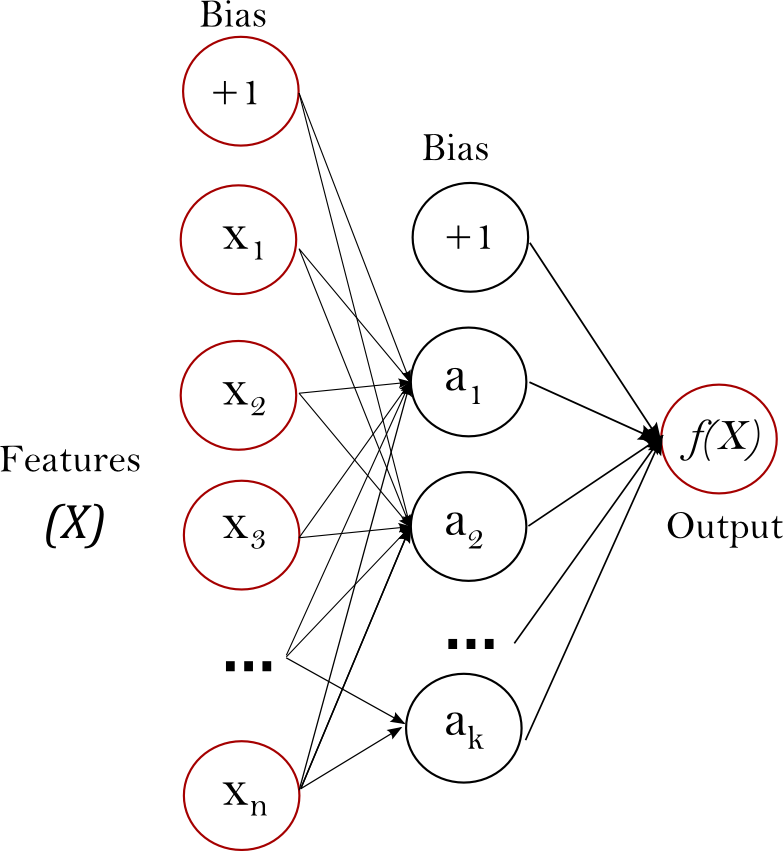
Figure ane : Ane hidden layer MLP. ¶
The leftmost layer, known as the input layer, consists of a gear up of neurons \(\{x_i | x_1, x_2, ..., x_m\}\) representing the input features. Each neuron in the hidden layer transforms the values from the previous layer with a weighted linear summation \(w_1x_1 + w_2x_2 + ... + w_mx_m\), followed past a non-linear activation function \(g(\cdot):R \rightarrow R\) - similar the hyperbolic tan part. The output layer receives the values from the last hidden layer and transforms them into output values.
The module contains the public attributes coefs_ and intercepts_ . coefs_ is a list of weight matrices, where weight matrix at index \(i\) represents the weights between layer \(i\) and layer \(i+one\). intercepts_ is a listing of bias vectors, where the vector at index \(i\) represents the bias values added to layer \(i+1\).
The advantages of Multi-layer Perceptron are:
Adequacy to learn non-linear models.
Capability to acquire models in existent-fourth dimension (on-line learning) using
partial_fit.
The disadvantages of Multi-layer Perceptron (MLP) include:
MLP with hidden layers have a not-convex loss function where there exists more than 1 local minimum. Therefore different random weight initializations can lead to different validation accuracy.
MLP requires tuning a number of hyperparameters such as the number of hidden neurons, layers, and iterations.
MLP is sensitive to feature scaling.
Please see Tips on Applied Use department that addresses some of these disadvantages.
ane.17.2. Classification¶
Class MLPClassifier implements a multi-layer perceptron (MLP) algorithm that trains using Backpropagation.
MLP trains on two arrays: array X of size (n_samples, n_features), which holds the training samples represented as floating betoken feature vectors; and assortment y of size (n_samples,), which holds the target values (class labels) for the training samples:
>>> from sklearn.neural_network import MLPClassifier >>> X = [[ 0. , 0. ], [ 1. , i. ]] >>> y = [ 0 , one ] >>> clf = MLPClassifier ( solver = 'lbfgs' , alpha = 1e-five , ... hidden_layer_sizes = ( v , 2 ), random_state = 1 ) ... >>> clf . fit ( 10 , y ) MLPClassifier(blastoff=1e-05, hidden_layer_sizes=(5, 2), random_state=one, solver='lbfgs') Later fitting (training), the model can predict labels for new samples:
>>> clf . predict ([[ 2. , 2. ], [ - 1. , - 2. ]]) array([1, 0]) MLP can fit a non-linear model to the grooming data. clf.coefs_ contains the weight matrices that constitute the model parameters:
>>> [ coef . shape for coef in clf . coefs_ ] [(ii, five), (5, 2), (2, i)] Currently, MLPClassifier supports only the Cross-Entropy loss function, which allows probability estimates by running the predict_proba method.
MLP trains using Backpropagation. More than precisely, it trains using some form of gradient descent and the gradients are calculated using Backpropagation. For classification, it minimizes the Cross-Entropy loss function, giving a vector of probability estimates \(P(y|x)\) per sample \(10\):
>>> clf . predict_proba ([[ ii. , 2. ], [ 1. , 2. ]]) array([[ane.967...e-04, nine.998...-01], [1.967...e-04, 9.998...-01]]) MLPClassifier supports multi-grade classification past applying Softmax as the output office.
Farther, the model supports multi-label classification in which a sample can belong to more than one form. For each class, the raw output passes through the logistic function. Values larger or equal to 0.5 are rounded to 1 , otherwise to 0 . For a predicted output of a sample, the indices where the value is one represents the assigned classes of that sample:
>>> X = [[ 0. , 0. ], [ 1. , ane. ]] >>> y = [[ 0 , 1 ], [ 1 , 1 ]] >>> clf = MLPClassifier ( solver = 'lbfgs' , alpha = 1e-five , ... hidden_layer_sizes = ( fifteen ,), random_state = ane ) ... >>> clf . fit ( X , y ) MLPClassifier(alpha=1e-05, hidden_layer_sizes=(xv,), random_state=ane, solver='lbfgs') >>> clf . predict ([[ one. , two. ]]) array([[ane, 1]]) >>> clf . predict ([[ 0. , 0. ]]) array([[0, 1]]) See the examples below and the docstring of MLPClassifier.fit for further information.
one.17.three. Regression¶
Class MLPRegressor implements a multi-layer perceptron (MLP) that trains using backpropagation with no activation function in the output layer, which can as well be seen equally using the identity function as activation function. Therefore, it uses the square error as the loss office, and the output is a set of continuous values.
MLPRegressor also supports multi-output regression, in which a sample can have more than than ane target.
ane.17.4. Regularization¶
Both MLPRegressor and MLPClassifier employ parameter alpha for regularization (L2 regularization) term which helps in avoiding overfitting by penalizing weights with big magnitudes. Post-obit plot displays varying decision part with value of alpha.
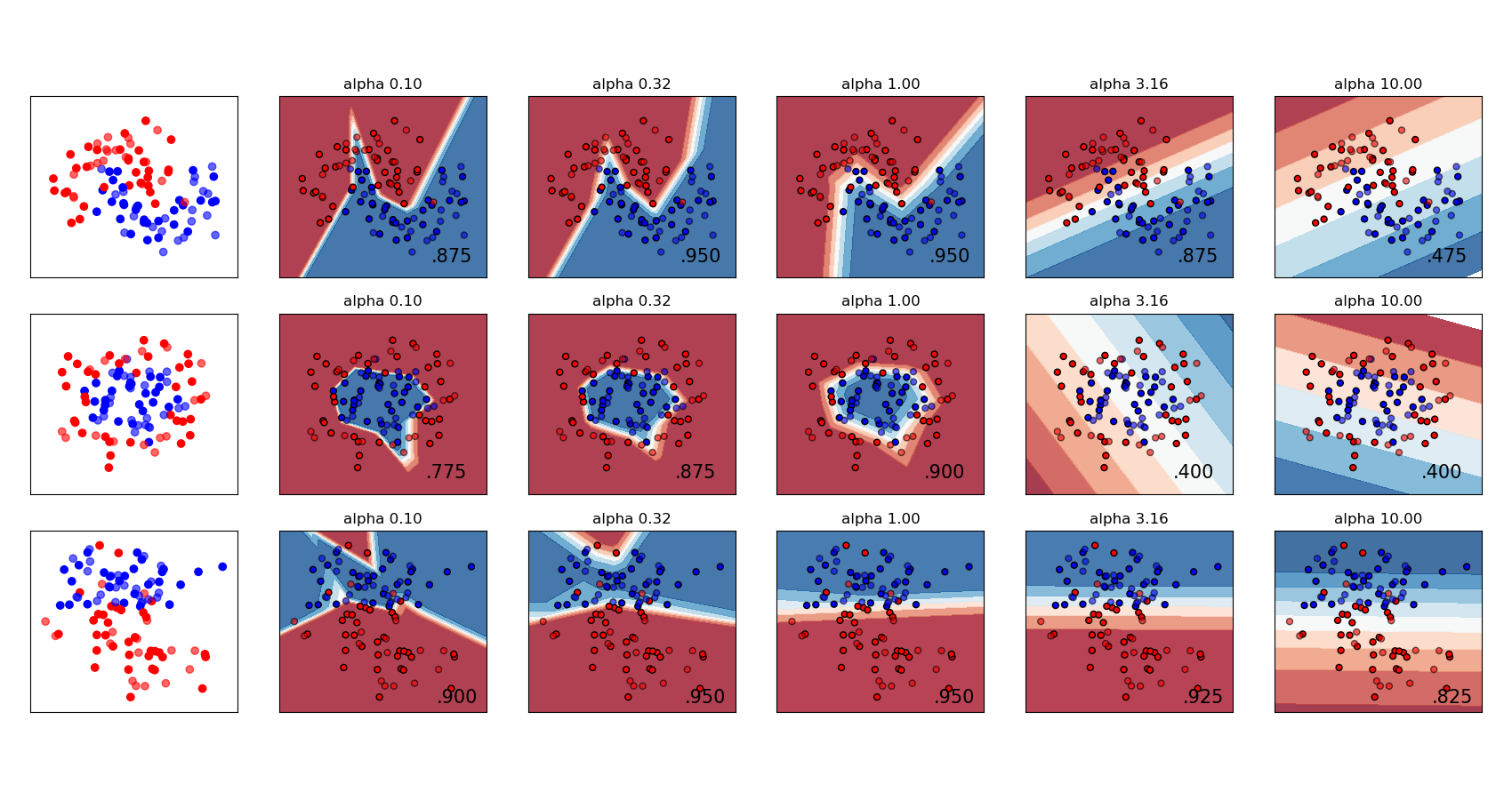
See the examples below for farther information.
1.17.5. Algorithms¶
MLP trains using Stochastic Gradient Descent, Adam, or 50-BFGS. Stochastic Gradient Descent (SGD) updates parameters using the gradient of the loss function with respect to a parameter that needs accommodation, i.e.
\[w \leftarrow westward - \eta (\alpha \frac{\partial R(westward)}{\partial westward} + \frac{\partial Loss}{\partial w})\]
where \(\eta\) is the learning charge per unit which controls the step-size in the parameter space search. \(Loss\) is the loss role used for the network.
More details tin can be found in the documentation of SGD
Adam is similar to SGD in a sense that it is a stochastic optimizer, but it tin can automatically conform the amount to update parameters based on adaptive estimates of lower-gild moments.
With SGD or Adam, grooming supports online and mini-batch learning.
L-BFGS is a solver that approximates the Hessian matrix which represents the second-club partial derivative of a part. Further information technology approximates the inverse of the Hessian matrix to perform parameter updates. The implementation uses the Scipy version of L-BFGS.
If the selected solver is 'L-BFGS', grooming does not support online nor mini-batch learning.
ane.17.6. Complexity¶
Suppose there are \(n\) preparation samples, \(m\) features, \(k\) hidden layers, each containing \(h\) neurons - for simplicity, and \(o\) output neurons. The fourth dimension complexity of backpropagation is \(O(n\cdot m \cdot h^yard \cdot o \cdot i)\), where \(i\) is the number of iterations. Since backpropagation has a loftier time complexity, it is appropriate to beginning with smaller number of hidden neurons and few subconscious layers for preparation.
1.17.7. Mathematical formulation¶
Given a set of training examples \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\) where \(x_i \in \mathbf{R}^n\) and \(y_i \in \{0, one\}\), a i subconscious layer one hidden neuron MLP learns the function \(f(x) = W_2 g(W_1^T 10 + b_1) + b_2\) where \(W_1 \in \mathbf{R}^m\) and \(W_2, b_1, b_2 \in \mathbf{R}\) are model parameters. \(W_1, W_2\) represent the weights of the input layer and hidden layer, respectively; and \(b_1, b_2\) stand for the bias added to the hidden layer and the output layer, respectively. \(yard(\cdot) : R \rightarrow R\) is the activation function, set by default as the hyperbolic tan. It is given as,
\[g(z)= \frac{e^z-e^{-z}}{e^z+east^{-z}}\]
For binary classification, \(f(x)\) passes through the logistic function \(g(z)=1/(1+eastward^{-z})\) to obtain output values between zero and one. A threshold, set to 0.v, would assign samples of outputs larger or equal 0.5 to the positive class, and the residue to the negative class.
If there are more than than two classes, \(f(x)\) itself would be a vector of size (n_classes,). Instead of passing through logistic office, it passes through the softmax part, which is written equally,
\[\text{softmax}(z)_i = \frac{\exp(z_i)}{\sum_{l=1}^k\exp(z_l)}\]
where \(z_i\) represents the \(i\) th element of the input to softmax, which corresponds to class \(i\), and \(K\) is the number of classes. The upshot is a vector containing the probabilities that sample \(x\) belong to each class. The output is the class with the highest probability.
In regression, the output remains as \(f(ten)\); therefore, output activation function is merely the identity function.
MLP uses dissimilar loss functions depending on the problem type. The loss role for nomenclature is Boilerplate Cantankerous-Entropy, which in binary case is given as,
\[Loss(\lid{y},y,W) = -\dfrac{ane}{n}\sum_{i=0}^n(y_i \ln {\chapeau{y_i}} + (1-y_i) \ln{(one-\hat{y_i})}) + \dfrac{\alpha}{2n} ||W||_2^two\]
where \(\alpha ||W||_2^two\) is an L2-regularization term (aka penalty) that penalizes complex models; and \(\alpha > 0\) is a non-negative hyperparameter that controls the magnitude of the penalty.
For regression, MLP uses the Hateful Square Error loss part; written every bit,
\[Loss(\hat{y},y,W) = \frac{one}{2n}\sum_{i=0}^n||\hat{y}_i - y_i ||_2^two + \frac{\alpha}{2n} ||West||_2^2\]
Starting from initial random weights, multi-layer perceptron (MLP) minimizes the loss role by repeatedly updating these weights. After computing the loss, a backward pass propagates it from the output layer to the previous layers, providing each weight parameter with an update value meant to decrease the loss.
In gradient descent, the gradient \(\nabla Loss_{W}\) of the loss with respect to the weights is computed and deducted from \(W\). More formally, this is expressed as,
\[W^{i+1} = W^i - \epsilon \nabla {Loss}_{West}^{i}\]
where \(i\) is the iteration pace, and \(\epsilon\) is the learning rate with a value larger than 0.
The algorithm stops when it reaches a preset maximum number of iterations; or when the improvement in loss is beneath a certain, small number.
1.17.eight. Tips on Practical Use¶
Multi-layer Perceptron is sensitive to feature scaling, so it is highly recommended to scale your data. For example, scale each attribute on the input vector X to [0, one] or [-1, +1], or standardize it to take hateful 0 and variance 1. Note that y'all must apply the same scaling to the test set for meaningful results. You can apply
StandardScalerfor standardization.>>> from sklearn.preprocessing import StandardScaler >>> scaler = StandardScaler () >>> # Don't crook - fit only on training data >>> scaler . fit ( X_train ) >>> X_train = scaler . transform ( X_train ) >>> # utilize same transformation to test data >>> X_test = scaler . transform ( X_test )An alternative and recommended approach is to use
StandardScalerin aPipelineFinding a reasonable regularization parameter \(\alpha\) is best done using
GridSearchCV, usually in the range10.0 ** -np.arange(1, 7).Empirically, we observed that
50-BFGSconverges faster and with better solutions on small-scale datasets. For relatively large datasets, however,Adamis very robust. Information technology usually converges quickly and gives pretty skillful performance.SGDwith momentum or nesterov's momentum, on the other paw, can perform meliorate than those two algorithms if learning rate is correctly tuned.
ane.17.nine. More than command with warm_start¶
If you want more command over stopping criteria or learning charge per unit in SGD, or want to exercise additional monitoring, using warm_start=True and max_iter=1 and iterating yourself tin exist helpful:
>>> X = [[ 0. , 0. ], [ 1. , ane. ]] >>> y = [ 0 , one ] >>> clf = MLPClassifier ( hidden_layer_sizes = ( 15 ,), random_state = one , max_iter = one , warm_start = True ) >>> for i in range ( 10 ): ... clf . fit ( X , y ) ... # additional monitoring / inspection MLPClassifier(... References:
-
"Learning representations by dorsum-propagating errors." Rumelhart, David E., Geoffrey Due east. Hinton, and Ronald J. Williams.
-
"Stochastic Gradient Descent" L. Bottou - Website, 2010.
-
"Backpropagation" Andrew Ng, Jiquan Ngiam, Chuan Yu Foo, Yifan Mai, Caroline Suen - Website, 2011.
-
"Efficient BackProp" Y. LeCun, Fifty. Bottou, G. Orr, K. Müller - In Neural Networks: Tricks of the Merchandise 1998.
-
"Adam: A method for stochastic optimization." Kingma, Diederik, and Jimmy Ba (2014)
How To Use Scikit Learn Mlp,
Source: http://scikit-learn.org/stable/modules/neural_networks_supervised.html
Posted by: smithupyrairow.blogspot.com


0 Response to "How To Use Scikit Learn Mlp"
Post a Comment